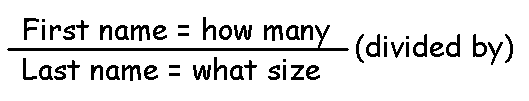Fractions
Fraction notation and operations may be the most abstract math monsters our students meet until they get to algebra. Before we can explain those frustrating fractions, we teachers need to go back to the basics for ourselves. First, let’s get rid of two common misconceptions:
- A fraction is not two numbers.
Every fraction is a single number. A fraction can be added to other numbers (or subtracted, multiplied, etc.), and it has to obey the Distributive Law and all the other standard rules for numbers. It takes two digits (plus a bar) to write a fraction, just as it takes two digits to write the number 18 — but, like 18, the fraction is a single number that names a certain amount of whatever we are counting or measuring.
- A fraction is not something to do.
A fraction is a number, not a recipe for action. The fraction 3/4 does not mean, “Cut your pizza into 4 pieces, and then keep 3 of them.” The fraction 3/4 simply names a certain amount of stuff, more than a half but not as much as a whole thing. When our students are learning fractions, we do cut up models to help them understand, but the fractions themselves are simply numbers.
Learn to Read a Fraction
A fraction is a number that relates to whatever is defined as one whole thing. Before a fraction can have any meaning, something has to be defined as “one whole unit.” Of course, this is true of all numbers, not just fractions. Before three can have any meaning at all, one has to be defined. Are we talking about 3 miles or 3 bags of rice or 3 spaces on the number line? Natural numbers are defined in terms of whatever one is, so fractions are no different from other numbers in this respect.
At the beginning, students need to make extensive use of fraction models. Let’s not limit ourselves to the round food model, but it is a great place to start. For the rest of this post, you may imagine “one whole unit” to be a single pizza, cut up into fractional pieces.
The first confusing thing about fractions is vocabulary: those awful wordsnumerator and denominator. To keep them straight, our students must learn how to read a fraction. Teach your children to read fractions from top to bottom, like the pages in a book:
- The top number of a fraction is its first name, which tells how many pieces you have.
- The line in a fraction means “divided by”, so 3/4 = 3 ÷ 4 and 5 ÷ 2 = 5/2.
- And the bottom number is the fraction’s last name or family name. It tells what size the pieces are.
Now, let’s go through that a little slower…
Numerator: The Fraction’s First Name
The top number in a fraction is its first name — that is, the first thing you hear about the fraction. A fraction’s first name counts the number of pieces: 2/5 has two pieces, and 3/5 has three of them.
This makes it easy to count up the total number of pieces in a bunch of fractions:
And if you add another fifth, that would make 8/5. Add a few more to get 11/5, then maybe take some away:
You can keep counting up and down forever, as long as you are only talking about fifths.
Mnemonic: It may help your students to think “number-ator.” The numerator counts thenumber of pieces we have.
Denominator: The Fraction’s Family Name
[Yes, this is out of order. We want our students to meet and get to know the fractions, so for beginners we focus on the names. Learning about the fraction bar comes later.]
The bottom number of a fraction is its last name, or family name. All fractions with the same last name are in the same family. The family name tells what size the pieces are — which is the same as saying how many of the pieces to make one whole thing. (Remember that fractions are always defined in relationship to some whole thing.) With fourths, it takes four of them to make a whole. With sevenths, it takes seven of them to make a whole thing.
This is why, as the last name gets bigger, the fraction itself gets smaller. The more pieces your whole thing has been cut into, the smaller each piece will be.
…because both have two pieces, but 7ths are smaller pieces than 4ths.
A man is like a fraction whose numerator is what he is and whose denominator is what he thinks of himself. The larger the denominator, the smaller the fraction.— Tolstoy
Mnemonic: It may help your students to think “down-nominator.” The denominator is the number down in the bottom of a fraction.
Put Them Together, and What Do You Get?
So what number is the fraction? It is the number that names the amount of stuff in all those pieces.
- The fraction 3/4 names the amount of pizza in 3 pieces, when each piece is 1/4 the size of one whole pizza.
- The fraction 13/5 names the amount of pizza in 13 pieces, when each piece is 1/5 the size of one whole pizza.
- The fraction 8/8 names the amount of pizza in 8 pieces, when each piece is 1/8 the size of one whole pizza.
But it is important to remember that the fraction itself is NOT the same as those pieces of pizza. If I had 3/4 of a pizza, it would be the same amount of stuff even if it had not been cut up — for instance, if my daughter came through and cut out as much of the pizza as she wanted, without bothering to cut the rest apart. And the whole pizza is 8/8 of a pizza, even before the first cut is made.
As we work our way toward a solid understanding of fraction operations, we will often come back to our fraction models to ask these questions:
- What size are the pieces?
- How many of them do we have?
The Line in a Fraction Means “Divided By”
Every fraction is also a division problem — or rather, it is the answer to a division problem. For instance, the fraction 7/3 names the amount of pizza each person would get, if we divided 7 pizzas evenly among 3 teenage boys:
Think of the division symbol “÷” as a miniature picture of a fraction. The dots stand for the numerator and denominator.
This is why the remainder in a division problem turns into a fraction. Consider those 3 teenage boys fighting over the 7 pizzas. It is easy to give them each 2 whole pizzas, but what shall we do with the remaining one? We have to cut it up, and each boy will get 1 ÷ 3 of it.
Whatever our remainder is, that becomes the numerator of our remainder-fraction. The denominator is whatever we were dividing by.
Knowing that the line in a fraction means “divided by” will be important in solving complex fractions like this MathCounts puzzler:
…or when our students meet algebra monster fractions like:
So we will keep reminding our students of this fact throughout middle school or junior high:
A fraction is a division problem.
source: http://letsplaymath.net/2007/11/07/how-to-read-a-fraction/
Improper Fractions
What is 9/8 ? Is that a fraction?
If we assume it into a daily problem like usual, a cake that we divide into 8 pieces then we take 9 of it? Is that possible?
The answer is yes, because it is an improper fraction.
Do you know what improper means?
It means "not right".
“You’ve got it! Fractions bigger than one just don’t seem right, do they? So he called themimproper fractions, and that’s what we still call them today.”
source: http://letsplaymath.net/2007/02/20/a-mathematical-trauma/
How to read a fraction?
We can read: three-fourth, three over four, or three divided by four.
The above bar is called numerator and the bellow bar is called denominator.
Examples:
1/2 = a half
1/3 = a/one third
1/4 = a/one quarter
1/25 = one twenty fifth
345/107 = three hundred fourty five over a hundred and seven. (We can use "over" if the number is too big.)
3 1/2 = three and a half
8 6/9 = eight and six ninth
0.5 = nought point five
0.46 = nought point four six
0.523 = nought point five two three
5.7 = five point seven
3.5 = three and a half
5.25 = five and a quarter
- With fractions below 1, we use of before nouns. Half is a little bit different.
three quarters of an houreight tenth of a milea fifth of students
- For decimals below 1, you can use of or a plural noun.
nought point seven of a mile = nought point seven miles
- Fractions and decimals over 1 are normally followed by plural nouns.
One and a half hours2.7 millimeters
- To express amounts and measurements, use singular verbs with fractions and decimals.
3.6 kilometer is about 2 miles.
- But to express numbers of people or things, use plural verbs.
Half the students are tired.A fifth of the tickets have been sold.
- We can use a or one. One is more formal.
a hundred (less formal)one hundred (more formal)
- A can only be used at the beginning of a number.
a/one hundredthree thousands one hundred , three thousands a hundred
source: http://englishresort.blogspot.com/2008/12/how-to-read-fraction.html
^_^ Selamat Belajar ^_^